• Home
• Crystallisation
• Synthesis
  Technology
  • Chiral
    Technology
  • Organic
    Synthesis
  • Route/Process
    R&D
• Pharmaceutical
  Profiling
• Intellectual
  Property
• Solid Solution
  Theory
• Entrainment
  Theory
• Resolution
  Calculator
• Purification
  Calculator

Theory for Modelling Resolution by Entrainment

Introduction
Entrainment Scenarios
Theory for Mathematical Modelling
Examples of Mathematical Modelling

Introduction

It is often possible to obtain in a crystallisation more of a desired crystal form than is thermodynamically favoured, by entraining with crystals of that form. Thus adding crystals of a compound to a supersaturated solution can selectively entrain its own form whilst other crystal forms of the same compound do not crystallise, and other compounds are likewise retained in solution. Taking advantage of this kinetic phenomenon can often result in improved process yields relative to that indicated from the measured solubilities. For an entrainment crystallisation to be effective, it is necessary that the desired and unwanted crystal forms do not twin, i.e. that the presence of the desired crystals does not promote crystallisation of the unwanted form. The effectiveness of an entrainment also has to take account of the likelihood of independent unwanted nucleation of the unwanted form being in supersaturated solution.

Entrainment Scenarios

Entrainment of a crystallisation may be useful in various circumstances and development of an entrainment process may be assisted by reference to a mathematical model. The following scenarios of increasing complexity may be considered:

1. Single compound A with two crystal forms A1 and A2, entrained by A1.
2. Two compounds A and B, each with one crystal form and entrained by A.
3. Two compounds A and B but that can also form an addition compound A-B.
4. Two compounds A and B, where A has two forms A1 and A2 and entrained by A1.
5. Two compounds A and B, where B has two forms B1 and B2 and entrained by A.
6. Two compounds A and B each with two forms.

The entrainment approach is valuable as a method for separating stereoisomeric compounds, and in particular for enantiomers (chiral isomers). The above Scenario 2 is then applicable where A and B are the (R)- or (S)-enantiomers and the entrainment is to effect a direct chiral resolution. Likewise this scenario may be to make a separation of diastereoisomeric compounds more effective. If the intent is to effect the direct resolution of an enantiomer by entrainment, then this might be compromised by the formation of a racemic-compound crystalline form that contains both enantiomers in the crystal and Scenario 3 applies. In this case such a resolution will only be effective if the crystals of the single enantiomer do not appreciably twin with the racemic-compound form. The more-complicated scenarios 4-6 can have unusual kinetic consequences since there may be relay effects of crystal forms promoting the crystallisation of others in sequence.

Theory for Mathematical Modelling

Suppose we have a mixture supersaturated in crystal forms 'A' and 'B' (which might be the same compound or not) and seeded(entrained) with form 'A'. Then to a first approximation it may be assumed that:  'A' will crystallise in proportion to its own amount of solid A_C, and its supersaturation in the solution A_S, so the rate of crystallisation of 'A' is given by Equation 1.

Equation 1.

However, if 'A' twins with form 'B' it will promote the crystallisation of 'B' in proportion to the amount of 'A' crystals and 'B' supersaturation according to Equation 2.

Equation 2.

A twinning parameter 'T' can be set being the propensity of 'A' to promote the crystallisation of 'B' relative to that of itself. That can be represented by Equation 3.

Equation 3.

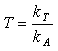
So Equation 2 can alternatively be written in the form of Equation 4.

Equation 4.

Once the crystallisation of form 'B' has started it will continue analogously to Equation 1, and the overall rate of crystallisation of 'B' can be written according to Equation 5.

Equation 5.

Analogously to Equation 3, it is also useful to take the ratio of rate constants for the self-propagated crystallisation of 'A' and 'B' , here termed 'U' according to Equation 6.

Equation 6.

Substituting this into Equation 5 then gives Equation 7.

Equation 7.

Finally, the rate of crystallisation of 'B' can be compared to that of 'A' by dividing Equation 7 by Equation 1. That gives Equation 8.

Equation 8.

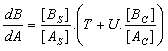
It is useful to model the entrainments by mathematic iteration computing the increments in the amounts of crystals of each form/compounds and the decrements in the concentration of the compounds in solution. It is convenient to have a time-increment factor i = k_A.dt; the value of which is chosen so that a complete profile of an entrainment can be visualised within the number of iterations chosen (say 200). Then Equations 9 and 10 are useful for building the model.

Equation 9.

Equation 10.

The above gives a model based on simple assumptions, but can be elaborated as follows, being customised for particular circumstances of a crystallisation-entrainment process:

1. If there are several crystal forms/compounds,an appropriately extended set of relative factors T and U, as defined above, can be used, with a correspondingly extended set of equations for the iteration.
2. The extent of entrainment is made proportional to a measure of the active surface area of crystals rather than simply the mass of them. Indeed, the active surface area will be proportional to the mass only if the crystals retain a constant average size through the crystallisation. An adjustment may be made by taking the mass of the crystals to an appropriate power, typically in the range 0.67 - 1.00; the lower value being if the entrainment is dominated by increase of crystal size rather than by increase of the crystal numbers.
3. Aside from the crystallisation of the second crystal form/compound being promoted by the amount of the first, the second crystal form could nucleate of its own accord if the solution is sufficiently supersaturated. Thus the calculation can take account of a metastable zone, within which spontaneous self-nucleation does not occur, but beyond which nucleation occurs to an extent dependent upon its degree of supersaturation.
4. The relationship between rate of crystallisation with extent of supersaturation (above a metastable zone or not) may be made to be other than linear, to match with particular experimental results.
5. The model can be made to take account of the possibility that the crystallisation of one crystal form/compound will obscure the crystals of the other. The assumption is that if a crystal form deposits, it can do so by either covering itself or cover the other form, depending on the relative proportions of the two forms in the crystal surface available and an obscurement factor O. The effect of the obscurement is to adjust the relative proportion of the two crystal forms in the active crystal surface area in accordance with point 2 above.
6. The way solubility varies with composition of the component compounds can be accommodated, in particular for the direct entrainment of a single enantiomer from its racemate, an important parameter is the ratio α, of the solubility of the racemate with that of a single enantiomer.
7. The model can take account of the changes in solubilities, crystallisation rates, and metastable zone widths with temperature if developing a crystallisation process in which the mixture is cooled as the crystallisation progresses.
8. Adjustment can be made for any extent of solid-solution formation between different compounds in a given crystal form.

Examples of Mathematical Modelling

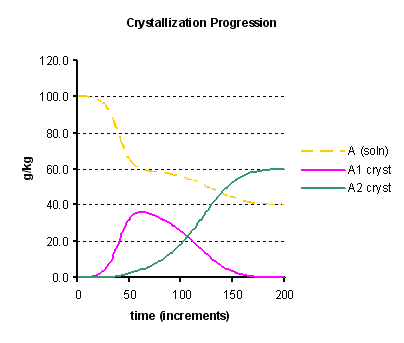
By applying the model to a simple scenario of a single compound with two crystal forms A1 and A2, starting with a solution supersaturated in both forms, but seeded with the more soluble one A1, we may obtain the profile shown in Figure 1 below. With a chosen set of parameters, the crystallisation is visualised to take place in two stages. In the first stage the seeded form A1 crystallises, and the liquors approach a concentration in A equal to the solubility of this crystal form. Because in this model the crystal form A1 promotes, to some extent the deposition of form A2, then this second form starts to crystallise out. Thereafter, the liquor concentration approaches the lower solubility of the second crystal form, and meanwhile the first form becomes under-saturated in solution and redissolves so that all the crystalline mass transforms into the second form.

Initial soln. conc. of A:

100 g/kg

Solubility of A1:

60 g/kg

Solubility of A2:

40 g/kg

U: relative rate of cryst. progression A2 vs A1:

0.50

T: relative induction rate of A2 by A1:

0.01

Initial A1 crystals:

0.10 g/kg

Initial A2 crystals:

0.00 g/kg

Increment factor i:

0.004

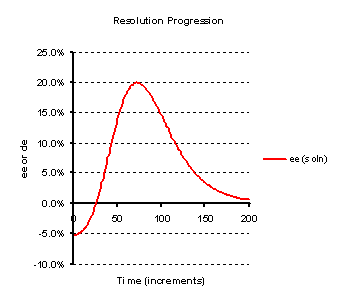
The following illustrations (Figures 2 to 3) are for the scenario of entrainment of a single enantiomer from a mixture of them, i.e. two compounds A and B here termed (R) and (S) as usual for enantiomers, each having one crystal form. Figure 2 models an entrainment where a solution, having a small excess of (S)-isomer is seeded with that isomer. The graph plots the enantiomeric excess of the compound in solution (the difference in the concentrations of the R and S isomers divided by their sum). First the (S)-isomer crystallises but does so beyond the point at which the liquors contain the same amount of each (racemic), so the sign of the enantiomeric excess changes. In practice this might be measured by the optical rotation of the solution which will be found to change sign. Then the entrainment of (S)-isomer will continue until the liquors reach a maximum enantiomeric excess in favour of (R) isomer, at which point the mixture would be harvested (the crystals collected) in the case of a process being developed. Beyond this point the (R)-isomer then crystallises and the liquor tends towards the most soluble racemic composition. In this example it is seen that the level of entrainment is so as to give a maximum entrainment with the liquors of 20% ee. The horizontal axis labelled as time is actually the number of iterations used in the model.

The modelling would be useful to predict the effect of changing various controllable conditions of the entrainment. For instance it predicts that by using a greater initial enantiomeric excess of the solution, would give a greater level of entrainment.

Initial solution conc. of (R):

90 g/kg

Initial solution conc. of (S):

100 g/kg

Sol. of single enantiomer:

40 g/kg

Sol. ratio enant/racemate, α:

2.00

A: surf. area rel volume power:

0.67

T: rel. induction rate (R) vs (S):

0.01

O: obscurement:

0.00

M: metastable zone, % of satd:

0.0%

N: nucl. rate beyond metastable:

0.00

Initial quantity of (R) crystals:

0.00 g/kg

Initial quantity of (S) crystals:

0.10 g/kg

Increment factor i:

0.004

It may also be used to show the effect of intrinsic physical parameters of the system, so for instance changing the value of the parameter α (the ratio of solubilities of the racemate to the single enantiomer) from 2 to 3 reduces the extent of entrainment to a maximum liquor ee of 11.5%.

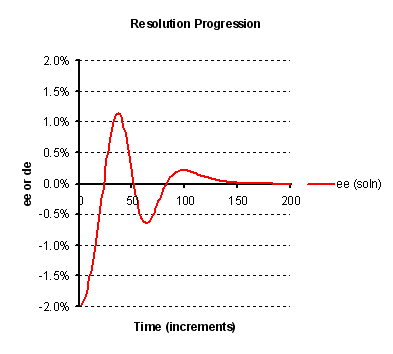
The illustration in Figure 3 below shows a possible effect of the crystallisation of one isomer obscuring the other. With a sufficiently high level of obscurement, the sign of the enantiomeric excess of the liquor may oscillate. In fact such as oscillation has been observed in practice in the entrainment crystallisation of 2-azabicyclo[2.2.1]hept-5-en-3-one (as described by A. Collet et al in Angew. Chem. Int. Ed., 1996, 35, 1666). Moreover, it is seen that in this case, according the model the extent of entrainment is poor, and indeed this was borne out in practise also.

Initial solution conc. of (R):

96 g/kg

Initial solution conc. of (S):

100g/kg

Sol. of single enantiomer:

40g/kg

Sol. ratio enant/racemate, α

2.00

A: surf. area rel volume power:

0.67

T: rel. induction rate (R) vs (S):

0.01

O: obscurement:

3.50

M: metastable zone, % of satd:

0.0%

N: nucl. rate beyond metastable:

0.00

Initial quantity of (R) crystals:

0.00 g/kg

Initial quantity of (S) crystals:

0.10 g/kg

Increment factor i:

0.004

The purpose of these examples are to show that the modelling approach can faithfully reproduce actual experimentally-observed scenarios and can therefore be a valuable tool in the development and optimization of crystallisation-based processes. The modelling approach can be customized for particular actual scenarios and in this regard if your organisation seeks assistance in the use of such modelling then please enquire at: enquiries@mcc-sci.com

The application of this modelling methodology alongside the experimental evaluation of the physical properties of the crystal forms in a crystallisation process can be provided in collaboration with: Park Place Research Ltd, who specialises in experimental Process R&D services with a particular emphasis on process analytical automation technology. This provides a complete solution for identifying an optimal crystallisation purification or separation process.