• Home
• Crystallisation
• Synthesis
  Technology
  • Chiral
    Technology
  • Organic
    Synthesis
  • Route/Process
    R&D
• Pharmaceutical
  Profiling
• Intellectual
  Property
• Solid Solution
  Theory
• Entrainment
  Theory
• Resolution
  Calculator
• Purification
  Calculator

Purification by Crystallisation

Introduction

Here is a calculator for predicting the results of a crystallisation purification when starting with a composition having a given percentage of an impurity and taken to a given yield of crystals. It takes account of both eutectic composition and solid-solution formation. Instructions for use of the calculator and discussion are given afterwards. Note that another calculator useful in crystallisation resolution is available on the Resolution Distribution Calculator page.

Calculator

CRYSTALLISATION PURIFICATION CALCULATOR

INPUT VALUES

• initial percentage
  of impurity
  
  
• relative solubility
  of impurity
  
  
• solid solution extent
  of the impurity in
  desired compound
  
• solid solution extent
  of desired compound
  in the impurity
  
• yield of
  crystals
  

CALCULATED VALUES

• percentage impurity
  in crystals
  
  
• percentage impurity
  in liquors
  
  
• 
  
  
  
• percentage impurity
  in eutectic
  

  please enter your data into the yellow cells of the input area

Instructions

To use the calculator enter your data in place of the initial default values given in the yellow cells of the 'INPUT VALUES' section and press the 'Calculate' button; corresponding calculated crystal-composition and liquor-composition values appear on the right, together with the composition of the eutectic between the components if one exists.

Of the Input Values:

1. The initial percentage of impurity will usually be entered as a small value (e.g. 5%) if a purification is being carried out, but it can accommodate any value upto 100%, so entering 50% would correspond to starting with a 1:1 mixture (e.g. for a resolution). However for resolution work it might be more appropriate to use the companion calculator in the page: Resolution Distribution Calculator.
2. The relative solubility is that of the isolated impurity divided by that of the desired compound; so a figure of 0.2 means that the impurity has one fifth of the solubility, whilst 5.0 means the impurity is five times more soluble than the desired compound. If concentrated solutions are used, the solubilities should be entered as weight/weight (e.g. g solute/kg solution); since then the decrease in weight of the solution when material crystallises is accounted for in the calculation
3. The solid solution extent phenomenon is described in the separate page on Solid Solution Theory. In the case of two components to be separated, a solid solution could in principle be formed by molecules of either component being accommodated within the crystal form of the other. The middle (third) input cell is for a percentage value for the solid solution extent of molecules of the impurity within the crystal structure of the desired compound. It can range from 0% (no solid-solution formed) to 100% (a complete solid solution in which the crystal structure does not distinguish the components. The extent of solid-solution is likely to be higher if the molecules concerned are structurally very similar. Presence of such a solid-solution will make it difficult to completely remove the impurity from the crystals by recrystallisation.
4. The next cell is for the extent of solid-solution of the desired compound within the crystal structure of the impurity. If the impurity is less soluble than the desired compound, this could have a profound effect on the efficiency of a crystallisation method.
5. The last input cell is for the yield of the crystallisation; i.e. the number of grams (or moles) of crystals compared with the starting composition. It is to be entered as a percentage. In a purification, the aim will be to maximise the crystallisation yield but the purity outcome is often very dependent on the yield and there will often be an optimal value

If an invalid value is entered, a message is given to indicate this and invalid value(s) are reset to the default figures. Otherwise the message indicates which crystal forms (the desired compound, the impurity or both) are calculated to deposit. If the solubility ratio and solid-solution extents allow a eutectic composition between the components, then the impurity percentage in that eutectic composition is given in the lower of three output cells. The calculated liquor composition will be equal to that figure if the starting composition and yield are such that the eutectic composition is reached.

Discussion

The Figure below shows an example of the use of the calculator with a ternary phase diagram represention of the scenario. In this example, where the solubilities of the (separated) desired component and impurity are 100 g/kg and 20 g/kg respectively (solubility ratio = 0.2) there is minimal purification by recrystallisation because the eutectic composition is near to the start position. The figure shows the path of the liquors (green line) from the starting composition to the eutectic point at the intersection of the (dashed) solubility lines of the two components. In other scenarios, the impurity might actually concentrate in the crystals, with the liquors being the purified stream.

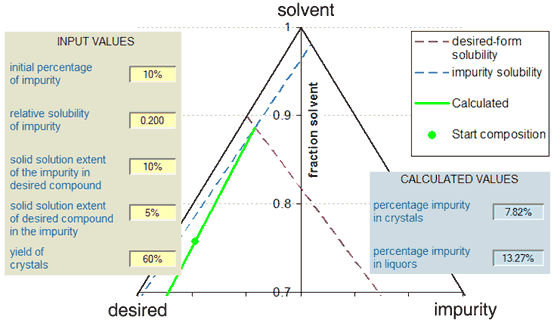
The calculator makes various assumptions, for instance in relation to the ideality of any solid-solution behaviour. With the ideal behaviour, the variation of the solubility of a component with composition is a straight line on the ternary phase diagram (as with the Figure above) and the slope of the line is in accordance with the extent of solid-solution formation. The result of any solid-solution formation will be to modify the position of the eutectic, which is given by the equation below. In this equation, F is the solubility ratio of the impurity to the desired compound and the two D-values are the solid-solution extents as described above. It is evident that in the absence of solid-solution formation, the percentage of the impurity in the eutectic is given simply by F/(1 + F). Another assumption made is that the results obtained represent equilibration with the various species, so if the crystals are produced by kinetic phenomena, the value of the calculation may be limited. In particular the calculator assumes that the crystal form or combination of crystal forms is deposited that has the least solubility.

This particular calculator only gives results in one direction; that is the crystal and liquor compositions from a given starting composition, yield and the solubility/solid-solution parameters. If those parameters are not known, trial and error can be used to fit them with given experimental results. However it could be necessary to use the results of several experiments in order to establish a consistent set of physical parameters so that the calculator can then effectively predict the results of experiments under further different conditions. In particular if the eutectic composition is sought, it is best to crystallise at high yield under conditions assuring equilibration whilst to measure a solid-solution extent it is best to crystallise at low yield from a mixture predominant in one or other of the components. Note that the calculator on the page Resolution Distribution Calculator can intercalculate between different choices of input variables, but does not take any account of eutectic compositions. If your particular task is more complex than can be accommodated directly with this calculator or has a high level of importance to your business then McCague Scientific Consulting is available to advise on specific projects through a consultancy mechanism.